Lambertian pattern of escaping light

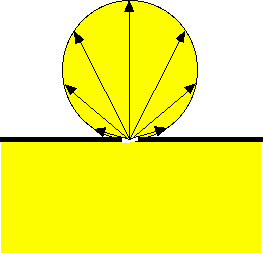
There is a common pattern to the angular distribution escaping light from certain diffuse sources. The so-called Lambertian pattern depends on the angle relative to the normal that is perpendicular to the surface of the source. For the case of radiant intensity I [W/sr], one can consider how I would vary as a function of the angle of observation:

• When observing the source perpendicular to the source's surface, cos = 1 and I( ) is maximal.
• When observing the source obliquely, cos < 1 and I( ) is submaximal, approaching zero as approaches 90 °.

Why is there a Lambertian pattern?

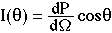
Our frosted light bulb has an inner light-scattering coating such that a large fraction of the light is backscattered into the bulb at a random angle. Multiple scattering of photons occurs within the bulb randomizing all photon trajectories and creating a uniform concentration of photons within the bulb volume. A small fraction of the light striking the bulb coating will transmit through the coating and escape the bulb.

An incremental area dA on the surface of the bulb behaves like a small window. A photon can strike the window and escape. But as a photon approaches the window, the target size presented by the window varies according to the factor cos, as illustrated below:

A photon approaching the window along axis z sees a large cross-section for escape (= dA).
A photon approaching the window along the vector a sees a foreshortened cross-section for escape (= dA cos).

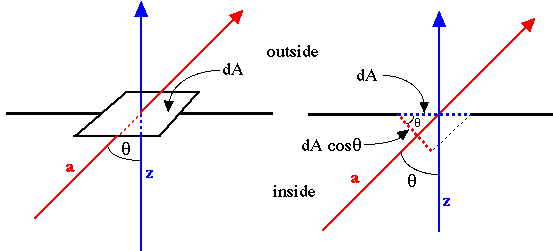
Consequently, if the angular distribution of photons approaching the window is uniform, i.e., the light bulb is filled with perfectly diffuse light, then the cross-section of the window target exerts its influence and the pattern of radiation transmitted through the window will show a cos dependence:

Radiation pattern for diffuse photons passing through a small window from a region of uniform concentration of photons with randomized trajectories. The circle illustrates the cos dependence of radiation.