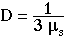|
ECE532 Biomedical Optics
© 1998
Steven L. Jacques, Scott A. Prahl
Oregon Graduate Institute |
Diffusion theory
Connecting optical transport theory and Fick's 1st law of diffusion.
The early work on neutron scattering theory in nuclear reactors first developed the connection between transport theory and Fick's 1st law of diffusion. The resulting statement of diffusion is also applied to optical transport. Consider the following problem:
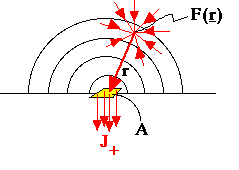
Light scattered at position r passes through a small aperture with area A contributing to the flux J+.
|
- given a homogeneous isotropically scattering medium with scattering coefficient µs
- given a small aperture with area A at the origin (r = 0)
- given a fluence rate F(0) at the origin
- assume that the fluence rate F(r) at a position r near to the aperture is approximated by
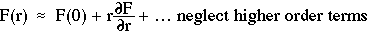
- calculate the net flux through the small aperture with area A due to scattering from all the surrounding volume:
- the scattered flux at r is µsF(r) = µs( F(0) + r(dF(r)/drat r=0) ) where r is the distance from r to the origin.
- the fraction of scattered flux from r that survives a pathlength r without being scattered or absorbed is exp(-µtr), where µt = µs + µa. Consider the case of negligible absorption compared to scattering so µt = µs.
- the fraction of surviving scattered flux from r that passes through A is Acosθ/(4πr2).
- integrate the flux from r over all possible θ and r for the hemisphere above the aperture:
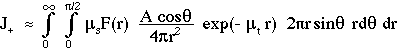
- a similar integration for the scattering from the hemisphere below the aperture yields a positive value J- for flux passing through A in the other direction opposite to J+.
- the net flux J = J+ - J-
- The final expression for the net flux J has the form of Fick's 1st law of diffusion if the diffusion constant D has the following value:
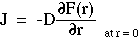 , where
, where 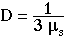
For photon transport, the term µs' = µs(1 - g) is substituted the above µs which described isotropic scattering used in the above treatment.
In summary, the connection between transport theory and Fick's 1st law of diffusion is based on the linearization of F(r) around the value F(0) and on the approximation of D by the value 1/(3 µs').
to next page |
Chapter 5 |
Course |
Home



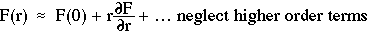
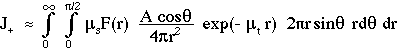
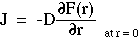 , where
, where