Step 4 of 8: Curvatures
We're using surplus lenses because they're cheap. The lenses, unfortunately don't have a specified radius of curvature or index of refraction. So we need to figure these out.
The lenses are probably made from BK-7 glass, but we really don't know. In any case the index will be close to 1.5 and the radius of curvature for the DCX lens will be $$ {1\over f} = (n-1)\left[{1\over R_\mathrm{DCX}} - {1\over -R_\mathrm{DCX}}\right]$$ or just $$ R_\mathrm{DCX} =f. $$
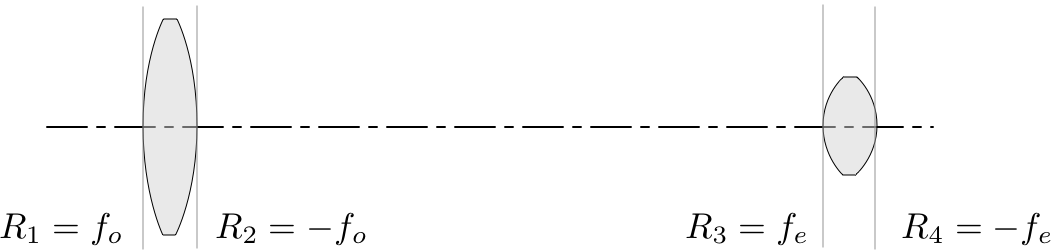
For the plano-convex lens, the second surface is flat so that surface has $R=\infty$. The radius of curvature of the curved surface is $$ R_\mathrm{PCX} = {f\over2}.$$
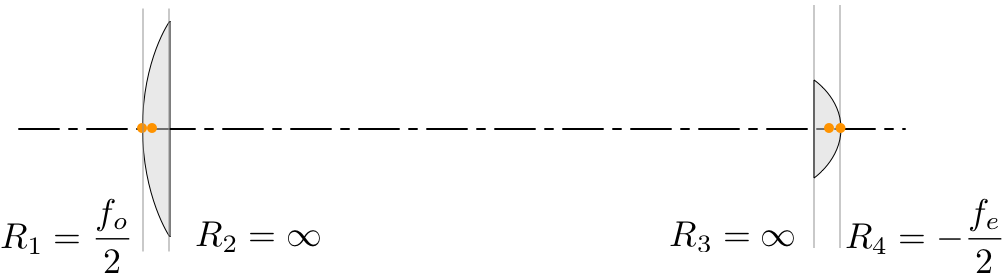
So for the lenses that we selected, the curvatures are
| $R_1$ | $R_2$ | $R_3$ | $R_4$ | |
|---|---|---|---|---|
| mm | mm | mm | mm | |
| DCX | 235 | -235 | 23 | -23 |
| PCX | 111 | $\infty$ | $\infty$ | -11 |
"Wait, wait!", you cry out, "What about the correction for a thick lens?" Recall the equation $$ {1\over f} = (n-1)\left[{1\over R_\mathrm{DCX}} - {1\over -R_\mathrm{DCX}} + {(n-1)t\over n R_\mathrm{DCX}^2}\right]$$ I whine, "But the equation is quadratic in $R_\mathrm{DCX}$!"
If $n=1.5=3/2$, after selecting the appropriate solution of the quadratic equation, we get $$R_\mathrm{DCX} = {f\over2}\left[ 1+ \sqrt{1-{2 t\over3f} } \right]$$ If $t\ll f$ and we can expand in $t$ to get $$R_\mathrm{DCX} \approx f-{t\over6}$$ Of course, this is approximation is invalid for the eyepiece lens.
Interestingly, there is no correction needed for the PCX lenses.
Plausible thicknesses for the DCX objective is 6mm and for the DCX eyepiece is 9mm. Plugging these in gives
| $R_1$ | $R_2$ | $R_3$ | $R_4$ | |
|---|---|---|---|---|
| mm | mm | mm | mm | |
| DCX | 234 | -234 | 21.4 | -21.4 |
| PCX | 111 | $\infty$ | $\infty$ | -11 |