Step 4 of 8: Find the curvature of each surface
We need to know the curvature of the first (AST) surface. The lensmaker's equation for a thin lens is
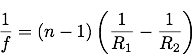
where, of course, R1 is the radius of curvature of the first surface, R2 is for the second surface, and f is the focal length of the lens. Now, since the lens is equi-convex, the radius of curvature of one side is the negative of the radius of the other side so R1=R=-R2 so
Now we can solve for the radius of curvature
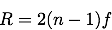
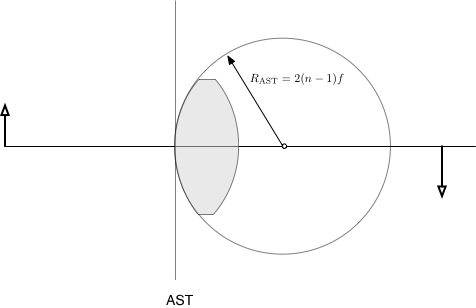
The radius of curvature of the first surface is positive because the sphere's center is to the right of the vertex.
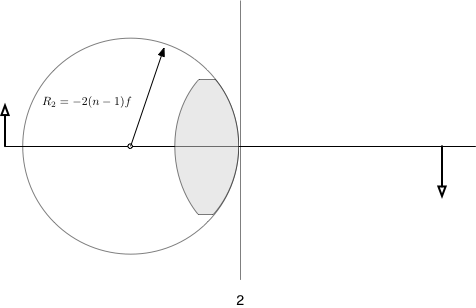
The second surface has a negative radius of curvature because the sphere's center is to the left of the vertex
The object and image surfaces also have radii of curvatures. Since they are flat, this corresponds to a circle that is infinitely big and so, of course, we write 0 (zero).
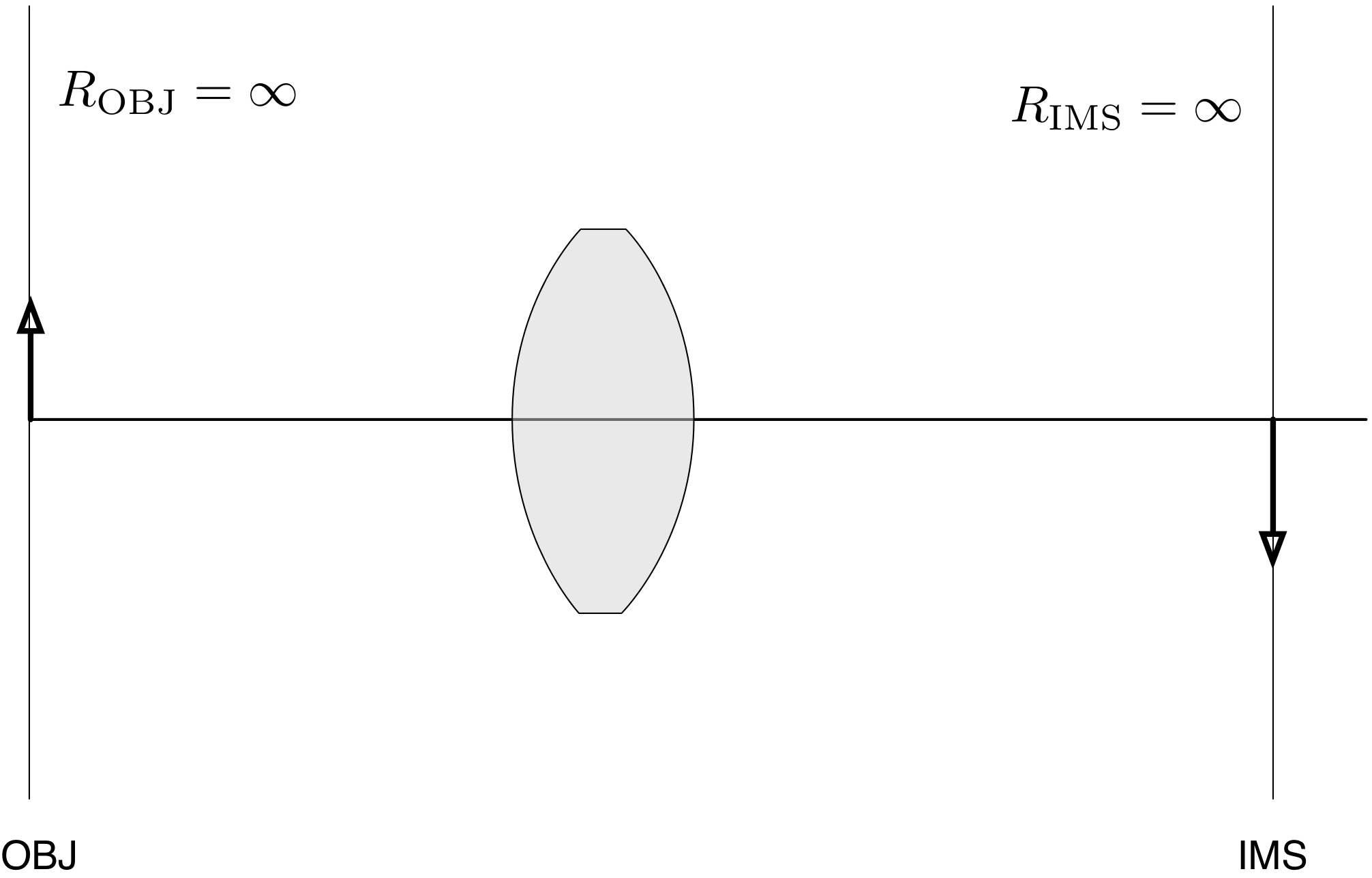
Now, collect all the curvatures in one place
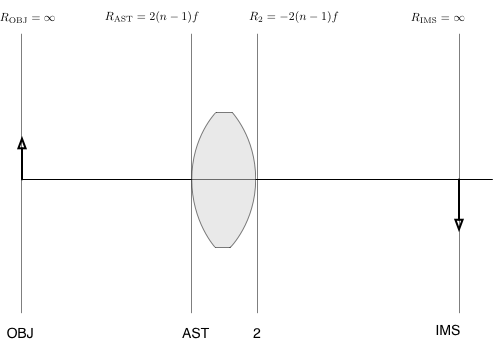
Collect these curvatures into a table describing your optical system.
| Surface | Curvature | Distance | Height | Material |
|---|---|---|---|---|
| OBJ | 0 | |||
| AST | Rast | |||
| 2 | R2 | |||
| IMS | 0 |